5. Potential calculations
5.1
Presentation
Capture cross sections can be calculated within the
potential-model formalism. Only electric multipoles are supported in
this release. The formula for the cross section is given, for instance, in
C. Angulo et al. , Nucl. Phys. A656 (1999) 3 (equation 19).
Several partial wave can be included.
Final results can be
used to compute the reaction rate.
5.2 Input data
At startup, the screen looks like:
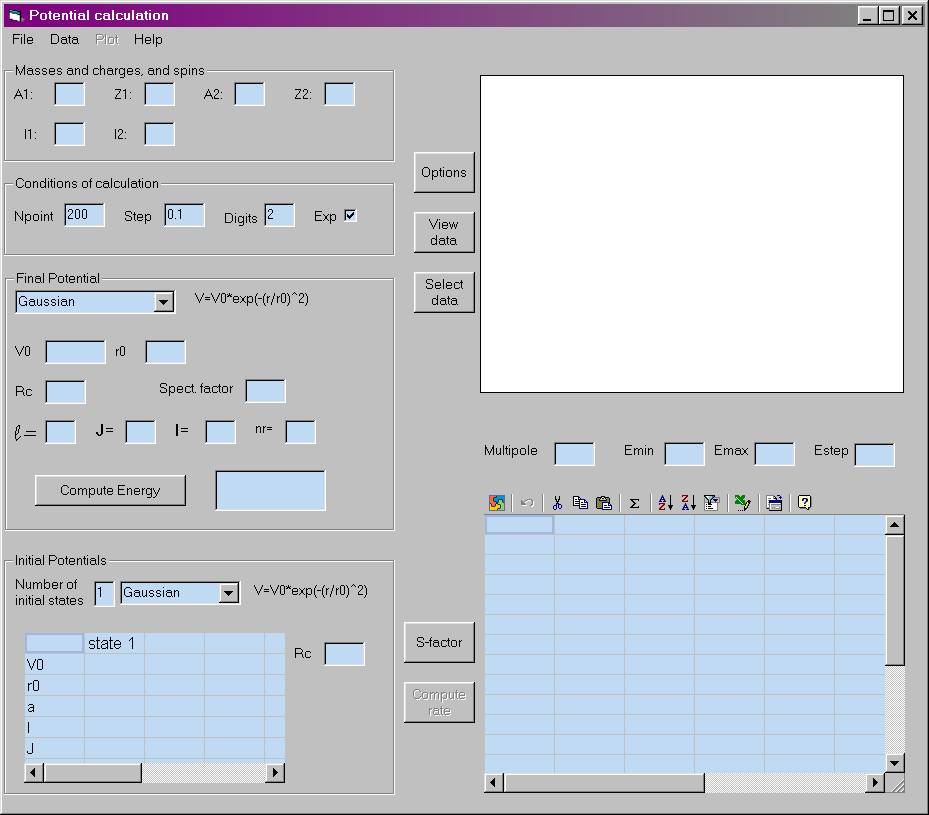
The procedure is the following:
a. Import a file
with non-resonant cross sections, or download it from The NACRE server.
b. Enter parameters of the final state:
- Npoint: number of points for the integration (typically 200, but some reactions such
as 7Be(p,g)8B for example need more points)
- h: step for integration (typically 0.1)
- Ndigits: nmber of digits for the S-factor
- Lf: final angular momentum
- Jf: initial total spin
- nr: number of nodes in the radial wave function
- Rc: radius of the sphere-radius Coulomb potential (typically
Rc=1.4*A1/3 fm)
- Enter the potential (gaussian or Woods-Saxon)
The energy of the final state can be checked at this stage. Before computing the rate
you can fit the potential parameters.
c. Enter parameters of the intial state(s):
- Choose the potential and the number of partial waves.
- Li: initial angular momentum
- Ji: initial total spin
- Give the potential parameters for each partial wave.
As usual, some selection rules must be taken into
account.
5.3 Results
Before computing the cross section, you have to give the order of the
multipole (electric) and the energies.
- l: order if the multipole
- Emin: minimum energy (in MeV)
- Emax: maximum energy (in MeV)
- Estep: energy step (in MeV)
The phase shifts, the cross sections and the S-factors
are then calculated.
5.4 Example: the
7Be(p,g)8B
reaction
- Experimental data can be imported but this is not
necessary (see the procedure described for R-matrix calculations).
- Enter Masses and charges, and number of points:
| Npoint=800 |
number of points |
| h=0.2 |
step |
- Enter data for the 8B ground state
| L=1 |
orbital angular momentum |
| J=2 |
initial spin |
| l=2 |
channel spin |
| nr=0 |
number of nodes in the wave function |
| Rc=2.39 |
Coulomb radius |
| V0=-46.87 |
depth of the Woods-Saxon potential |
| r0=2.39 |
range of the Woods-Saxon potential |
| a=0.65 |
diffuseness |
Check that
the ground-state energy is -0.136 MeV.
- Enter the parameters of the initial potentials (2
states: l=0 and l=2).
| V0=-46.87 |
depth of the Woods-Saxon potential |
| r0=2.39 |
range of the Woods-Saxon potential |
| a=0.65 |
diffuseness |
| Li=0 and 2 |
orbital angular momentum |
| Ji=2 |
initial spin |
| Rc=2.39 |
Coulomb radius |
Note the the channel spin must be equal in the initial and
final states. It is therefore given for the final state only.
- Enter the multipole and energies
| l=1 |
multipole |
| Emin=0.1 |
first energy |
| Emax=1.0 |
final energy |
| Estep=0.1 |
energy step |
- The resulting S-factor is given here. Try
smaller values for Npoint (200 for example) to realize the sensitivity of
the S-factor.

