4. R-matrix calculations

4.1 Presentation

Capture cross sections can be calculated with the R-matrix formalism. Transfer cross sections are not supported by the release. Also only one partial wave can be included. You must repeat the calculation for each partial wave individually.

Input data are observed values, which correspond to experimental data. The link between observed and calculated parameters is performed as explaind in Ref. (C. Angulo and P. Descouvemont, Phys. Rev. C60,...,2000). External contribution is taken into account.

The program performs fits of the data starting from approximate paramater values.
Final results can be used to compute the reaction rate.

4.2 Input data

At startup, the screen looks like:

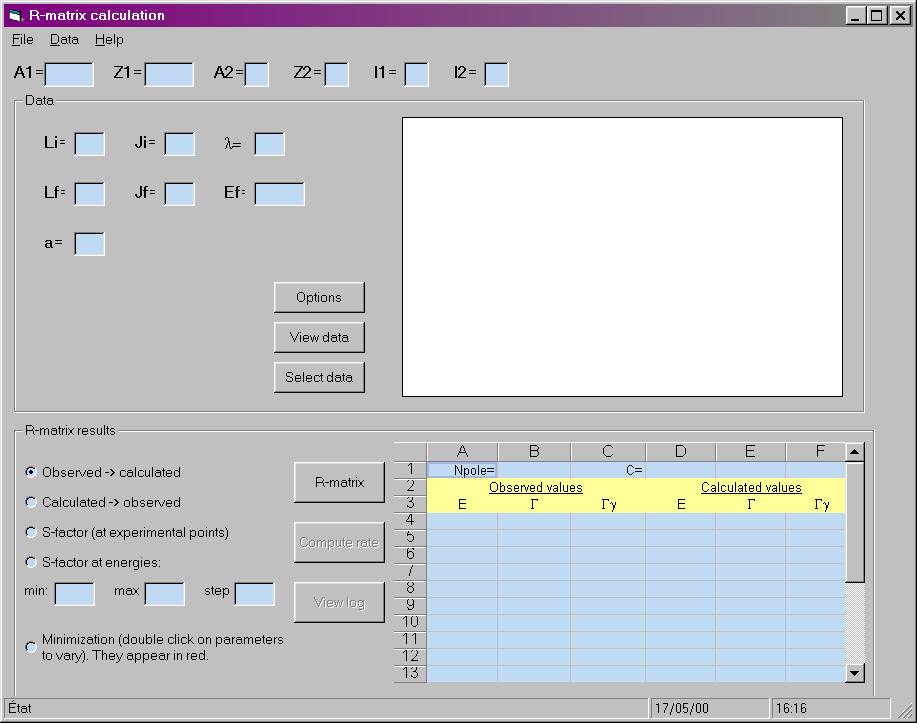
The procedure is the following: 
a. Import a file with non-resonant cross sections.

b. Enter parameters of the system:

• Li: initial angular momentum
• Ji: initial total spin
• l: order if the multipole
• Lf: final angular momentum
• Jf: initial total spin
• Ef: energy of the final state (negative, in MeV)
• a: channel radius (in fm)

As usual, some selection rules must be taken into account.

c. Give the number of poles (NPOLE) in cells B1

d. From line 4 to line 3+NPOLE, give the pole parameters: energy, reduced and gamma width (all in MeV). The gamma widths can be negative to account for interference effects.
If the reduced width is negative, the input parameter is considered as the total particle width (only for positive-energy states).

e. If the external correction is taken into account, the spectroscopic factor C must be given in cells D1.

4.3 Results

Different usages can be considered:
a. Compute calculated values from observed values (or reverse)

b. Compute the S-factor at the experimental energies or at given energies.

c. Perform a fit of the data (more lengthy!)
To select the parameters on which the minimization is applied, double-click on the corresponding cells. They appear in red, which means that this parameter is allowed to vary during the minimization. All other parameters remain fixed.

4.4 Example: the ¹²C(a,g)¹⁶O reaction (E2)

1. Import the data file c12ag.nr,  which contains some data about the E2 part of the  ¹²C(a,g)¹⁶O S-factor.
   
2. Enter data for this reaction
   
   

   Li=2	orbital angular momentum in the initial state
   Ji=2	initial spin (=Li since a and 12C have spin zero)
   l=2	multipolarity
   Lf=0	orbital angular momentum in the initial state
   Jf=0	final spin of 16O
   Ef=-7.16	binding energy of 16O with respect to the threshold
   a=6.5	channel radius

   
   
3. The calculation is perfomed with 4 poles (Npole=4). Their values are:
   
   

   pole 1	-0.24	0.2	9.70e-8
   pole 2	2.68	-6.25e-4	-5.70e-9
   pole 3	4.36	-0.073	6.1e-7
   pole 4	10.0	3.5	2.0e-5

   
   pole 2 and 3: the particle widths (negative) correspond to the total a widths
   
   
4. The resulting S-factor is given here.